Трендовые линии имеют интересное свойство: проявлять себя на графиках с логарифмической ценовой шкалой (а не арифметической). Если в абсолютном отношении на графике можно наблюдать ускорение роста цены (или замедление падения), то на этом же графике но с относительной (т.е. логарифмической) шкалой цен, вероятно, проявится отчетливая линия тренда. Следовательно, стоит просматривать график ценной бумаги в обоих режимах ценовой шкалы (логарифмическом и арифметическом) для поиска трендовых линий.
Напомним, что логарифмическая шкала цен показывает относительный прирост; на такой шкале, разница между отметками 10 и 20 равна разнице между отметками 20 и 40 (40 и 80, 80 и 160 и т.д. ), т.к. у обеих пар разница измеряется в относительном отношении; то есть разница во всех парах одинаковая, и составляет 100%. На шкале все эти разницы имеют одинаковое расстояние. А на арифметической шкале, разница между этими парами чисел была бы существенной, т.к. арифметическая шкала измеряет прирост абсолютный.
Вот пример для сравнения. На двух диаграммах изображен график цены на акции EMC Corporation (EMC). Период отображения — одинаковый: рост с 1998 по 2001 год.
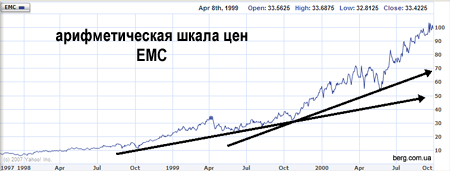
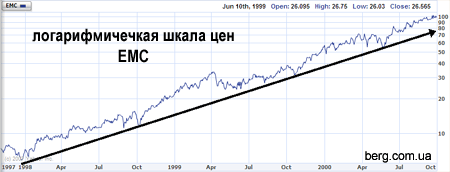
Обратите внимание: за 2 с половиной года цена акций увеличилась в 10 раз. Для того, чтоб провести восходящие трендовые линии на арифметическом графике, потребовалось бы 2 (или более) трендовых линий. Но на графике с логарифмической шкалой цен, идеально вписывается одна восходящая линия тренда, которая описывает экспоненциальный прирост цены акции EMC.



Мне кажется что логарифмическая шкала удобна для анализа очень длинных отрезков чисел и времени