Стандартне відхилення — класичний індикатор мінливості з описової статистики.
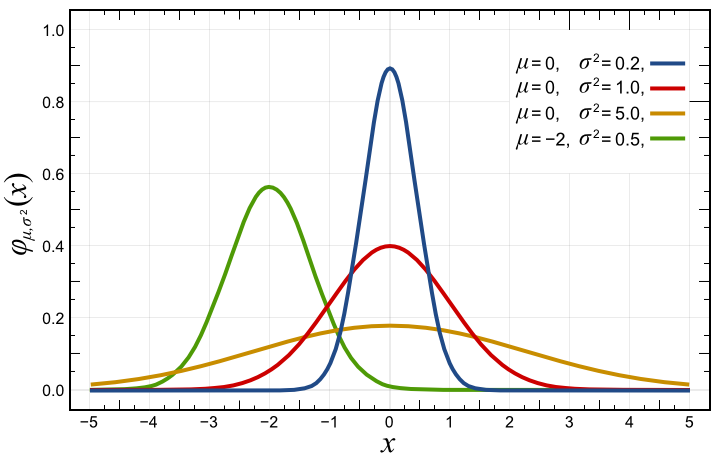
Стандартне відхилення, середньоквадратичне відхилення, СКО, вибіркове стандартне відхилення (англ. standard deviation, STD, STDev) — дуже поширений показник розсіювання в описовій статистиці . Проте, т.к. технічний аналіз схожий на статистику, даний показник можна (і потрібно) використовувати в технічному аналізі для виявлення ступеня розсіювання ціни аналізованого інструменту в часі. Позначається грецьким символом Сігма “σ”.
Дякую Карлам Гауссу та Пірсону за те, що ми маємо можливість користуватися стандартним відхиленням.
Використовуючи стандартне відхилення в технічному аналізі, ми перетворюємо цей “показник розсіювання” на “індикатор волатильності“, зберігаючи сенс, але змінюючи терміни .
Що таке стандартне відхилення
Розуміння суті стандартного відхилення можливе з розумінням азів описової статистики. Наприклад, маємо 2 вибірки, які мають середнє арифметичне однаково і дорівнює 3. Здавалося б, однакове середнє робить ці дві вибірки однаковими. Ан-ні! Давайте розглянемо можливі варіанти даних цих двох вибірок:
- 1, 2, 3, 4, 5
- -235, -103, 3, 100, 250
Очевидно, що розкид (або розсіювання, або, у нашому випадку, волатильність) набагато більший у другій вибірці. Отже, незважаючи на те, що у цих двох вибірок однакове середнє (рівне 3), вони абсолютно різні в силу того, що у другої вибірки дані безладно і сильно розсіяні навколо центру, а у першої – сконцентровані навколо центру та впорядковані.
Але якщо нам треба швидко дати зрозуміти про таке явище, ми не пояснюватимемо, як в абзаці вище, а просто скажемо, що у другої вибірки дуже велике стандартне відхилення, а у першої — дуже маленьке . Так, у другої вибірки стандартне відхилення дорівнює 186, а у першої воно дорівнює 1,6. Різниця суттєва.
Стандартне відхилення в технічному аналізі
Стандартне відхилення використовується в технічному аналізі не так часто, але воно є відмінним індикатором волатильності (мінливості). Стандартне відхилення використовується для проміжних обчислень різних індикаторів, таких як Смуги Боллінджера або Ширіна Полос Боллінджера.
Але крім проміжних допоміжних обчислень, стандартне відхилення є цілком прийнятним для самостійного обчислення та застосування в технічному аналізі. Як відзначив активний читач нашого журналу burdock, “досі не зрозумію, чому СКО не входить до набору стандартних індикаторів вітчизняних дилінгових центрів“.
Справді, стандартне відхилення може класичним та “чистим” способом виміряти мінливість інструмента. Але, на жаль, цей індикатор не настільки поширений у аналізі цінних паперів.
Застосування стандартного відхилення
Для будь-якого індикатора нам знадобиться змінна, тобто. параметр. В даному випадку нам потрібен лише період n, який вказує, яку кількість періодів ми включатимемо у обчислення стандартного відхилення.
Для обчислення ми беремо дані закриття з n періодів тому від останньої доступної ціни. Тобто. якщо ми встановили період індикатора 20 (досить часто використовуваний період), ми беремо 20 останніх даних і оперуємо ними для обчислення стандартного відхилення сьогодні. Отже, для обчислення стандартного відхилення в будь-який момент часу k, треба взяти ціни закриття всіх n періодів тому від k.
Обчислення стандартного відхилення
Попереджаю, що самостійне обчислення вам навряд чи знадобиться, тому що. основні програми обробки даних мають вбудовану функцію обчислення стандартного відхилення. Наприклад, у Microsoft Excel ця функція називається STDEV.
Вручну визначити стандартне відхилення не дуже цікаво, але корисно для досвіду. Стандартне відхилення можна виразити формулою STD=√[(∑(x-x)2)/n], що звучить як корінь із суми квадратів різниць між елементами вибірки та середнім, поділеної на кількість елементів у вибірці.
Якщо кількість елементів у вибірці перевищує 30, то знаменник дробу під коренем набуває значення n-1. Інакше використовується n.
Покроково обчислення стандартного відхилення:
- обчислюємо середню арифметичну вибірку даних
- віднімаємо це середнє від кожного елемента вибірки
- всі отримані різниці зводимо у квадрат
- сумуємо всі отримані квадрати
- ділимо отриману суму на кількість елементів у вибірці (або на n-1, якщо n>30)
- обчислюємо квадратний корінь з отриманого приватного (іменованого дисперсією)
Для наочності, ось приклад з таблиці Excel:
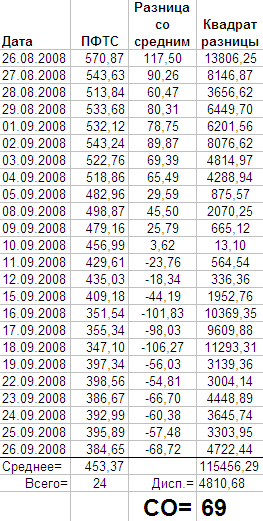
Початковий файл Excel додається (.xls 24kb).
У цьому прикладі я взяв короткий відрізок історичних даних цін закриття індексу ПФТС. Для обчислень дата не потрібна, але я вирішив її залишити, щоб ви могли звірити, якщо хочете. Що справді важливо, це все інше. Зверніть увагу на окремі дані під темним роздільником: “середнє” та “всього”. Є стовпець із ціною закриття, стовпець із різницями даних та середнього, і квадрати цих різниць.
Після обчислення квадратів ми складаємо їх, отриману суму ділимо на кількість елементів вибірки (оскільки всього елементів 24, що менше 30) і з отриманого чесного обчислюємо квадратний корінь. Результат округляємо до цілого і отримуємо 69.
Важливо помітити, що всі ці обчислення дадуть нам лише значення індикатора «стандартне відхилення» в останній день, тобто 26.09.2008, а для кожної іншої дати треба робити цей комплекс операцій окремо.
Прикладне значення стандартного відхилення
Нагадаю, що сенс стандартного відхилення полягає у виявленні ступеня мінливості інструменту. Тобто стандартне відхилення не зможе показати аналітику нічого, окрім волатильності.
Важливо зазначити, що елементи вибірки в середньому відрізняється від середнього значення на ±CO. Тобто. з прикладу вище, ціни закриття індексу ПФТС у середньому від середнього значення на ±69.
З прикладу вище, окремо цифра 69 нічого не скаже, тому що треба її використовувати з іншими значеннями стандартного відхилення в інші періоди. 69 — відносно чимала волатильність, але якщо в інші періоди стандартне відхилення буде більше 100, то, природно, 69 виявиться помірною мінливістю. Тобто “все пізнається в порівнянні“.
Висновок
Стандартне відхилення — це класичний індикатор мінливості з описової статистики. Він допоможе побачити, як змінюється волатильність інструменту у часі.






перший пост українською